
単位が取れるようにわかりやすい参考書が知りたいな。

院試勉強用の参考書は何を選べばいいのだろう?
微分積分・解析学の参考書はたくさんあり、どれを選べば良いか迷うものです。
そこで、レベル別・用途別におすすめの微分積分・解析学の参考書・問題集をランキングにしました。
レベル別・用途別は以下のように分けています。
- 初学者向け参考書
- 演習・定期テスト対策向け問題集 (中級者)
- 院試対策用問題集
- 基礎が理解できるための微分積分・解析学の参考書
- その人に合った微分積分・解析学の参考書
- 院試勉強用の微分積分・解析学の問題集
- 参考書を10%OFFで買えるサービス
1. 初学者向け

まずは、初学者用の参考書について紹介していきます。
初学者の定義やランキングの基準は以下の通りです。
- 微分積分・解析学を独学で学ぼうとしている人
- 大学の授業で微分積分・解析学の基礎を理解できなかった人
- 初学者にとって簡単でわかりやすいもの
- 初学者に必要な範囲の単元の網羅性

参考書ごとにどんな人に向いているか書いてあるので、自分に合ったものを選べるように参考にしてください。
1位 単位が取れる微積ノート
| 難易度 | 初学者向け | |
| わかりやすさ | 端的でわかりやすい | |
| 単元の網羅性 | 初学者には十分 |
1. 参考書の特徴
- 大学の単位が取れるがコンセプト
- 講義感覚で1セクション10ページの構成
2. 内容の特徴
- 初学者に必要な範囲を網羅
- 実際の試験問題に即した問題を収録
3. 説明の特徴
- 難しい用語や記号を丁寧に解説
- 図が多いのでイメージしやすい
- 程よい計算の補足
講義01 有理数と無理数
講義02 さまざまな関数1
講義03 さまざまな関数2
講義04 関数の極限
講義05 微分の定義
講義06 微分の計算
講義07 ロピタルの定理
講義08 テイラー展開とマクローリン展開
講義09 微分法の応用
講義10 不定積分
講義11 定積分
講義12 定積分の応用
講義13 空間座標
講義14 偏微分の定義
講義15 偏微分の計算
講義16 接平面と全微分
講義17 極点の決定
講義18 重積分
講義19 重積分と変数変換
- 独学で微積分・解析学を理解したい人
2位 1冊でマスター 大学の微分積分
| 難易度 | 初学者向け | |
| わかりやすさ | 図が多くてわかりやすい | |
| 単元の網羅性 | 初学者には十分 |
1. 参考書の特徴
- 演習問題も多く1冊でマスターがコンセプト
- 大学の単位を取るのに効率的な本
2. 内容の特徴
- 厳密な証明だけでなく、感覚的に公式を証明
- 約大問130問分の演習問題
3. 説明の特徴
- 図が多く、イメージしやすい
- 式の変形などがいい感じに丁寧
第1章 まずは高校の復習から
第2章 1変数の微分
第3章 1変数の積分
第4章 極限
第5章 2変数関数の微分
第6章 2変数関数の積分
第7章 ε‐δ論法に挑戦
第1章 まずは高校の復習から
1 極限の記号
2 自然対数の底e
3 三角関数の極限
4 逆関数
5 双曲線関数
第2章 1変数の微分
1 微分の計算法則
2 具体的な関数の微分の公式
3 微分の計算法則(応用編)
4 関数のグラフの描き方
第3章 1変数の微分
1 積分の計算法則
2 有理関数・三角関数・無理関数の積分
3 定積分
4 面積・体積・曲線の長さ
第4章 極限
1 数列の極限
2 無限級数
3 関数の極限の求め方
4 平均値の定理からテイラーの定理まで
第5章 2変数関数の微分
1 偏微分
2 全微分
3 2変数関数の極値
4 ラグランジュの未定乗数法
第6章 2変数関数の積分
1 重積分
2 重積分の変数変換
3 重積分の応用
第7章 ε−δ論法に挑戦
1 ε−δ論法
2 ε−δ論法の応用問題
- 感覚的に公式を理解したい人
- 演習問題もセットでたくさんこなしたい人
3位 微分積分キャンパス・ゼミ (マセマ)
| 難易度 | 初学者向け | |
| わかりやすさ | 丁寧でわかりやすい | |
| 単元の網羅性 | 初学者には十分 |
1. 参考書の特徴
- 大学生が1番使っているマセマシリーズ
2. 内容の特徴
- 初学者に必要な範囲を網羅
3. 説明の特徴
- 数式の解説が丁寧
- 公式の難しい表現や式を簡単に説明
- 難しい用語や記号を丁寧に解説
講義1 数列と関数の極限
1.数列の極限とε-N論法
2.正項級数とダランベールの判定法
3.三角関数と逆三角関数
4.指数・対数関数と双曲線関数
5.関数の極限とε-δ論法
講義2 微分法とその応用(1変数関数)
1.微分係数と導関数
2.微分計算
3.ロピタルの定理と関数の極限
4.微分法と関数のグラフ
5.テイラー展開とマクローリン展開
講義3 積分法とその応用(1変数関数)
1.不定積分
2.定積分
3.定積分のさまざまな応用
講義4 2変数関数の微分
1.2変数関数と偏微分
2.偏微分の計算と高階偏導関数
3.接平面と全微分
4.テイラー展開と極値
講義5 2変数関数の重積分
1.重積分
2.変数変換による重積分
- 計算が苦手な人
- 講義で微積分・解析学を理解できなかった人

単位が取れる微積ノートと著者が同じなので、範囲や図などが似ています。
大きな違いは、計算の説明の丁寧さの違いなので、好みに応じて選ぶと良いでしょう。
2. 演習用・定期テスト対策

次に、演習用・定期テスト対策用の問題集について紹介していきます。
このセクションでのターゲットとランキングの基準は以下の通りです。
- 基礎が理解できている人
- 院試や定期テストを見据えて、問題演習したいと思っている人
- 解説が丁寧で中級者が理解しやすいもの
- 問題の質 (院試や定期テストで頻出な良問)
- 問題量と単元の網羅性
1位 チャート式 微分積分
| 難易度 | 基礎から応用 | |
| 解説の丁寧さ | とても丁寧 | |
| 問題の質 | 良問揃い | |
| 問題量 | 大問300問程度 | |
| 単元の網羅性 | 工学部の院試に十分 |
1. 問題集のスタイル
- 大学受験でも有名なチャートの大学版
- ☆1~3の3段階のレベル別
(☆1超基礎,☆2 基本,☆3 標準~応用)
2. 問題の特徴
- 頻出の基礎問題から応用問題まで
- 問題パターンが多く、院試対策にも十分
- ε-N論法や級数に関しても詳しい
3. 解説の特徴
- 整頓されたわかりやすい解説
- 補足や注、参考など解説が丁寧
→つまずきにくいし、プラスαで学べる
- 問題を解く指針も書いてある
第1章 実数と数列
第2章 関数(1変数)
第3章 微分(1変数)
第4章 積分(1変数)
第5章 関数(多変数)
第6章 微分(多変数)
第7章 積分(多変数)
第8章 級数
第9章 微分方程式
第1章 実数と数列
1 実数の連続性
2 数列の収束と発散
3 単調数列とコーシー列
4 発展:上極限と下極限
5 発展:小数展開
第2章 関数(1変数)
1 関数の極限
2 極限の意味
3 関数の連続性
4 初等関数
第3章 微分(1変数)
1 微分可能性と微分
2 微分法の応用
3 ロピタルの定理
4 テイラーの定理
第4章 積分(1変数)
1 積分の概念
2 積分の計算
3 広義積分
4 積分法の応用
5 発展:リーマン積分
第5章 関数(多変数)
1 ユークリッド空間
2 多変数の関数
第6章 微分(多変数)
1 多変数関数の微分
2 微分法の応用
3 陰関数
4 発展:写像の微分
5 発展:微分作用素
第7章 積分(多変数)
1 重積分
2 重積分の応用
3 広義の重積分とその応用
4 発展:重積分の存在
第8章 級数
1 級数
2 整級数
3 整級数の応用
第9章 微分方程式
1 微分方程式の基礎
2 線形微分方程式
- 院試対策(工学部はこれで十分)
- 定期テスト対策
2位 演習 微分積分キャンパス・ゼミ (マセマ)
| 難易度 | 基礎的な問題が中心 | |
| 解説の丁寧さ | とても丁寧 | |
| 問題の質 | 良問 | |
| 問題量 | 大問150問程度 | |
| 単元の網羅性 | 基本的なことは網羅 |
1. 問題集のスタイル
- 大学生が1番使っているマセマシリーズ
- 1大問1ページ以上の丁寧な解説
2. 問題の特徴
- 定期テストの典型問題が中心
- 各公式の証明問題も多い
→いいアウトプットになる
3. 解説の特徴
- 丁寧すぎる数式(途中式)解説
- 解説が穴埋め式もあり
講義1 数列と関数の極限
講義2 微分法とその応用
講義3 積分法とその応用
講義4 2変数関数の微分
講義5 多変数関数の重積分
講義1 数列と関数の極限
数列の極限とε‐N論法 (問題1~6)
正項級数とダランベールの判定法 (問題7~10)
三角関数と逆関数 (問題11~16)
指数・対数関数と双曲線関数 (問題17~19)
関数の極限とε-δ論法 (問題20~23)
関数の連続性とε-δ論法 (問題24,25)
三角・指数・対数関数の極限 (問題26~29)
講義2 微分法とその応用
指数・対数関数の極限 (問題30,31)
微分計算 (問題32~41)
対数微分法と高階導関数 (問題42~45)
関数の極限とロピタルの定理 (問題46~51)
グラフの概形 (問題52~55)
関数のマクローリン展開 (問題56~61)
講義3 積分法とその応用
不定積分の計算 (問題62~72)
定積分の計算 (問題73~79)
広義積分と無限積分 (問題80~82)
面積・体積・曲線の長さ (問題83~91)
講義4 2変数関数の微分
2変数関数の極限と連続性 (問題92,93)
偏導関数・偏微分係数の計算 (問題94~101)
関数の全微分と接平面 (問題102~105)
全微分と変数変換 (問題106~109)
2変数関数のテイラー・マクローリン展開 (問題110,111)
2変数関数の極値 (問題112~115)
ラグランジュの未定乗数法 (問題116,117)
講義5 多変数関数の重積分
累次積分 (問題118~120)
広義の重積分・無限積分 (問題121~124)
変数変換による重積分 (問題125~131)
立体の体積 (問題132~135)
曲面の体積 (問題136~139)
3重積分 (問題140~143)
- 定期テスト対策用
- 初歩的なことをアウトプットしたい人
3位 弱点克服 大学生の微積分
| 難易度 | 基礎的 | |
| 解説の丁寧さ | 丁寧でわかりやすい | |
| 問題の質 | 高校の復習問題が多い | |
| 問題量 | 大問200問程度 | |
| 単元の網羅性 | 微積分に特化 |
1. 問題集のスタイル
- 弱点克服がコンセプトの問題集
- 文系の人にも理解してもらえるように執筆
2. 問題の特徴
- 微分積分の問題に特化
- 高校の復習が多く収録(4割ぐらい)
- 問題があって、その練習問題がある
→1つ1つ理解しやすい形式
3. 解説の特徴
- 解説でつまずきそうな所も丁寧に解説
- 問題に対する考え方も書いてある
Chapter 1 1変数関数の微分法
Chapter 2 1変数関数の積分法
Chapter 3 多変数関数の微分法
Chapter 4 多変数関数の積分法
Chapter 1.1変数関数の微分法
問題01 右方極限・左方極限
問題02 不定形の極限
問題03 重要な極限値(1)
問題04 重要な極限値(2)
問題05 はさみうちの原理
問題06 関数の連続
問題07 微分係数の定義
問題08 連続性と微分可能性
問題09 有理関数の微分法
問題10 無理関数の微分法
問題11 三角関数の微分法
問題12 指数関数・対数関数の微分法
問題13 対数微分法
問題14 逆三角関数
問題15 逆三角関数の微分法
問題16 双曲線関数の微分法
問題17 媒介変数による微分法、陰関数の微分法
問題18 第2次導関数
問題19 高次導関数
問題20 ライプニッツの公式
問題21 ロルの定理と平均値の定理
問題22 コーシーの平均値の定理
問題23 ロピタルの定理
問題24 テイラー展開
問題25 マクローリン展開
問題26 関数の近似式
コラム 1 ε-δ論法とランダウの記号
Chapter 2.1変数関数の積分法
問題27 1次式型の不定積分
問題28 分数関数の不定積分
問題29 逆三角関数になる不定積分
問題30 定積分の基本
問題31 置換積分法(1)――丸見え型
問題32 置換積分法(2)――無理関数
問題33 置換積分法(3)――超越関数
問題34 置換積分法(4)――三角関数による置換
問題35 部分積分法(1)
問題36 部分積分法(2)
問題37 部分積分法(3)
問題38 不定積分と漸化式
問題39 ∫sinnx dx ∫cosnx dx の積分計算
問題40 有限区間における異常積分
問題41 無限区間における異常積分
問題42 ベータ関数
問題43 ガンマ関数
問題44 級数の和の極限値
問題45 定積分と不等式
問題46 面積の基本
問題47 媒介変数表示の曲線の面積
問題48 極座標表示の曲線の面積
問題49 断面積を利用する体積
問題50 回転体の体積
問題51 回転体の体積(バーム・クーヘン型,斜回転体)
問題52 曲線の弧長
問題53 極座標表示の曲線の弧長
コラム 2 定積分の練習のススメと組立除法
Chapter 3.多変数関数の微分法
問題54 2変数関数の極限
問題55 2変数関数の連続
問題56 偏導関数
問題57 高次偏導関数
問題58 調和関数
問題59 偏微分係数
問題60 合成関数の偏導関数(1)
問題61 合成関数の偏導関数(2)
問題62 合成関数の偏導関数(3)
問題63 証明問題(1)
問題64 証明問題(2)
問題65 全微分
問題66 偏微分法における近似式
問題67 全微分における関数決定
問題68 偏微分法におけるテイラーの定理
問題69 偏微分法におけるマクローリン展開
問題70 2変数の関数の極値(1)
問題71 2変数の関数の極値(2)
問題72 陰関数における第2次導関数
問題73 陰関数の極値
問題74 条件つき極値問題
問題75 包絡線
問題76 接平面
コラム 3 多変数関数のグラフを見ておこう
Chapter 4.多変数関数の積分法
問題77 くり返し積分(1)
問題78 くり返し積分(2)
問題79 2重積分(1)
問題80 2重積分(2)
問題81 積分順序の変更(1)
問題82 積分順序の変更(2)
問題83 3重積分の基本
問題84 極座標への変数変換(1)
問題85 極座標への変数変換(2)
問題86 代表的な積分変数の変換
問題87 一般の積分変数の変換
問題88 3重積分における積分変数の変換
問題89 2重積分における広義積分(1)
問題90 2重積分における広義積分(2)
問題91 有名な広義積分
問題92 重積分による面積
問題93 2重積分を利用する体積(1)
問題94 2重積分を利用する体積(2)
問題95 3重積分と体積
問題96 曲面積
問題97 回転体の曲面積(側面積)
問題98 平面図形の重心
問題99 線積分
問題100 グリーンの定理
- 微積分学・解析学でつまずいている人
- 文系出身の人
3. 院試対策向け

最後に、院試対策向けの問題集について紹介していきます。
ランキングの基準は以下の通りです。
- 地方国公立~旧帝大レベル向けのもの
- 解説の丁寧さ
- 問題の質
- 問題量と単元の網羅性
1位 詳解 大学院への数学 微分積分編
| 難易度 | 地方国公立~旧帝大レベル | |
| 解説の丁寧さ | かなり丁寧 | |
| 問題の質 | 良問揃い | |
| 問題量 | 大問110問程度 | |
| 単元の網羅性 | 院試典型範囲をほぼ網羅 |
1. 問題集のスタイル
- 院試問題をとても丁寧に解説していく1冊
- 基本・標準・発展の3段階のレベル別
2. 問題の特徴
- 地方国公立~旧帝大から出題
- 基本問題 : 院試典型レベル
- 標準問題 : 院試やや難問レベル
- 発展問題: 院試難問レベル
- ε-N論法はないが、それ以外の単元は豊富
3. 解説の特徴
- 初歩から公式などを解説
→微積分・解析学が苦手な人にもわかる解説
- 問題を解くポイント・出題者の意図も解説
- 公式の図形的な意味も解説
→公式の理解が深まる
第1章 1 変数の微分
第2章 関数のべき級数展開
第3章 1変数の積分
第4章 多変数の微分
第5章 重積分
第6章 極値の問題
第7章 図形への応用
微分積分の基本公式
練習問題の略解
- 院試対策
- 微分積分・解析学の理解を深めたい人
2位 詳解 大学院への数学 理学工学系入試問題集
| 難易度 | 地方国公立~旧帝大レベル | |
| 解説の丁寧さ | やや簡潔 | |
| 問題の質 | 院試の典型問題が多数 | |
| 問題量 | 全大問400問 微分積分 : 70問 | |
| 単元の網羅性 | 院試典型範囲は網羅 |
1. 問題集のスタイル
- 地方国公立~旧帝大の数学の入試問題集
2. 問題の特徴
- 工学系に必要な数学のほとんどが収録
- 院試の頻出問題が多い
- 工学系の入試問題が中心
3. 解説の特徴
- 解説は基礎ができていないと理解が厳しい
- 1. 微分方程式
- 2. ラプラス変換、フーリエ解析
- 3. ベクトル解析
- 4. 微分、積分
- 5. 線形代数
- 6. 確率、統計
- 7. 複素関数
- 8. 情報・管理工学系の数学
- 1冊で院試数学の対策をしたい人
- 工学系の院試で数学が必要な人
3位 微分積分 (大学院入試問題から学ぶシリーズ)
| 難易度 | 応用問題以上しかない | |
| 解説の丁寧さ | 丁寧 | |
| 問題の質 | 院試の難問が厳選 | |
| 問題量 | 大問60問程度 | |
| 単元の網羅性 | かなり広い |
1. 問題集のスタイル
- 院試問題をとても丁寧に解説していく1冊
2. 問題の特徴
- ほとんどが東大の院試問題
- かなり込み入った問題が多い
- ニッチな範囲も網羅
3. 解説の特徴
- 問題の解説だけでなく、発展的なことも記載
第0章 基本問題でウォーミングアップ
第1章 関数と極限
第2章 微分法
第3章 積分法
第4章 偏微分法
第5章 重積分法
第6章 関数列と展開
- 理学部の旧帝大以上を受験する人
- 東大を受験する人
4. 参考書を10%OFF で買う方法

4.1 Amazon Prime Student 6ヶ月無料体験
参考書が安くなったらいいのになと思ったことありませんか?
Amazon Prime Student に登録すれば、なんと参考書を最大10%OFFで買うことができます。

私は大学生の時、約3万円分の参考書を買ったので、3000円お得になることになります。
6ヶ月間は無料体験期間として試せるので、無料で3000円もらえるようなものです。
さらに、Prime Studentは他にもたくさんのサービスを受けることができます。
- Prime Video
(映画やアニメが見放題)
- 便利な配送サービス
(お急ぎ便・日時指定など)
- Amazon Music Prime
(1億曲以上の曲をシャッフル再生で)
- Prime Before You Buy
(自宅で試着可能)
- Prime Reading
(1000冊以上の本が無料)
- Amazon Photos
(写真を容量無制限で保存)
prime studentの特典のすべては以下の通りです。
- 本最大10%ポイント還元
- Prime Video
(映画やアニメが見放題) - 便利な配送サービス
(お急ぎ便・日時指定など) - Amazon Music Prime
(1億曲以上の曲をシャッフル再生で) - Prime Before You Buy
(自宅で試着可能) - Prime Reading
(1000冊以上の本が無料) - Amazon Photos
(写真を容量無制限で保存) - 対象の文房具・ノートの割引
- ソフトウェアの対象商品割引
- Amazon MastercardでAmazonポイントが2%たまる
- お得なセールをいち早くチェック
- Amazon フレッシュ
- 無料体験期間が6か月
それぞれの特典やprime studentについてさらに詳しく知りたい方は以下の記事をご覧ください。
4.2 登録方法
① Prime Student 会員の登録ページにアクセスする
② 今すぐ開始をタップする

③ Amazonのアカウントにログイン
メールアドレスやパスワードを記入して、ログインします。
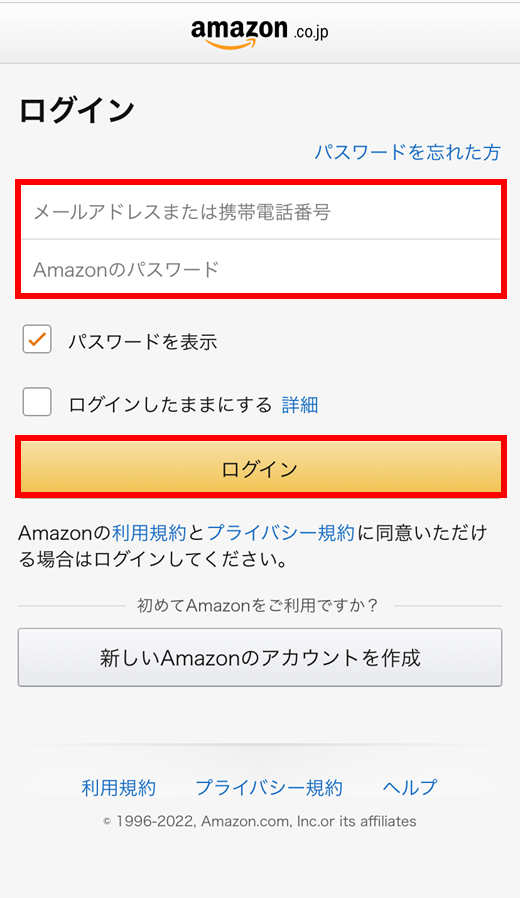
(ⅰ) 新しいAmazonのアカウントを作成をタップします。

(ⅱ) 氏名、メールアドレス、パスワードを記入して、次に進むをタップします。
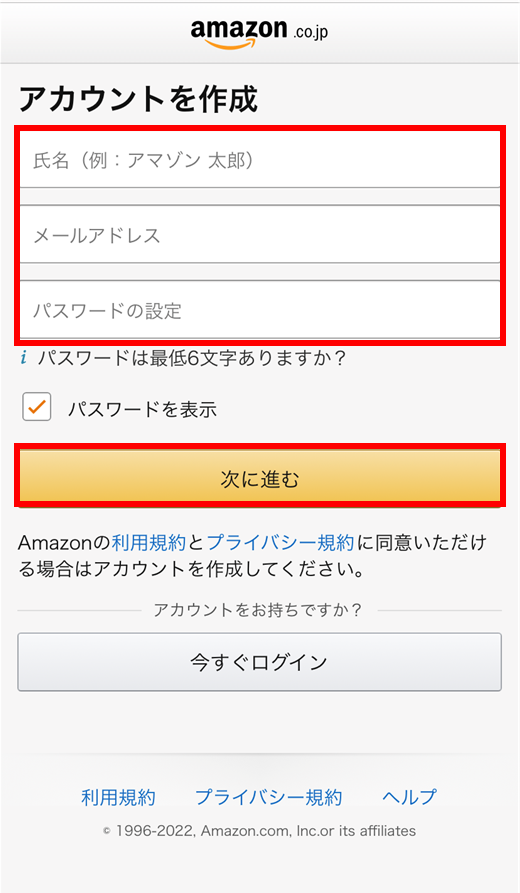
(ⅲ) 先程記入したメールアドレスに確認コードが届くのでそちらを画面に従って記入して下さい。
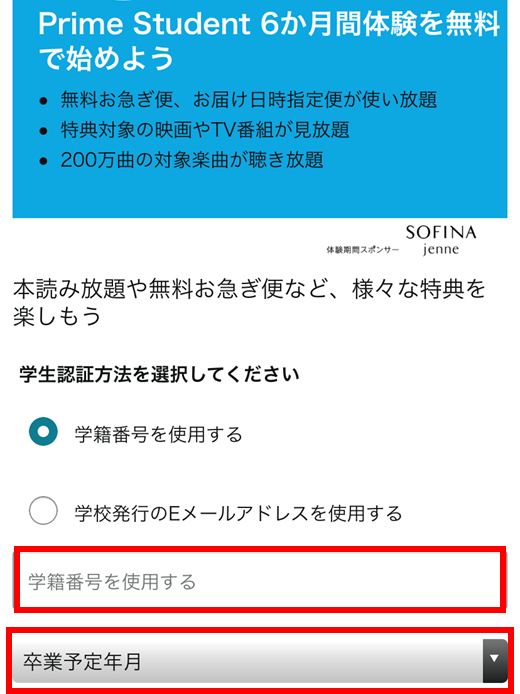
④ 学生認証
(ⅰ) 学生認証方法を選び、記入して下さい。
(ⅱ) 卒業予定年月を選択して下さい。
⑤ お支払い方法の選択と記入
お支払い方法を選択し、それぞれの指示に従って必要事項を記入して下さい。
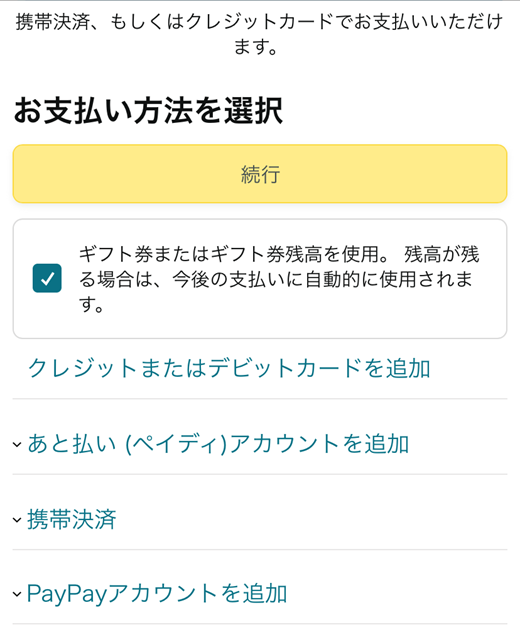
記入が終わったら、6ヶ月の体験期間を試すをタップすれば登録完了です。
5. 迷ったらこれ

5.1 初学者

難しい用語や記号を丁寧に解説し、端的にわかりやすくまとめられています。
5.2 演習用・定期テスト対策

大学受験でも有名なチャートの大学版で、とても扱いやすいです。
5.3 院試対策用

問題のレベルが幅広く、解説もかなり丁寧で、微積分・解析学の理解が深まります。












