
単位が取れるようにわかりやすい参考書が知りたいな。

院試勉強用の参考書は何を選べばいいのだろう?
複素関数(解析)の参考書はたくさんあり、どれを選べば良いか迷うものです。
そこで、レベル別・用途別におすすめの複素関数(解析)の参考書・問題集をランキングにしました。
レベル別・用途別は以下のように分けています。
- 初学者向け参考書
- 演習・定期テスト対策向け問題集 (中級者)
- 院試対策用問題集
- 基礎が理解できるための複素関数(解析)の参考書
- その人に合った複素関数(解析)の参考書
- 院試勉強用の複素関数(解析)の問題集
- 参考書を10%OFFで買えるサービス
1. 初学者向け

まず、初学者用の参考書について紹介していきます。
初学者の定義やランキングの基準は以下の通りです。
- 複素関数(解析)を独学で学ぼうとしている人
- 大学の授業で複素関数(解析)の基礎を理解できなかった人
- 初学者にとって簡単でわかりやすいもの
- 初学者に必要な範囲の単元の網羅性

参考書ごとにどんな人に向いているか書いてあるので、自分に合ったものを選べるように参考にしてください。
1位 1冊でマスター 大学の複素関数
| 難易度 | 初学者向け | |
| わかりやすさ | 簡単にかみ砕いて説明 | |
| 単元の網羅性 | 必須項目を網羅 |
- 理解から演習まで1冊で完結することを目的とした参考書
- 難しい方法をできるだけ避けて説明
- 無駄な項目が少なく、必須項目のみ
→混乱なく話が入りやすい
- 簡単に解く方法や考え方も書いてある
- 細かい数学の議論もされている
第1章 複素数平面と複素関数
- 1 複素数の計算
- 2 複素数平面
- 3 複素数の関数
第2章 指数関数・三角関数・対数関数
- 1 べき級数
- 2 指数関数・三角関数
- 3 対数関数
第3章 複素関数の微分
- 1 微分の定義
- 2 正則関数
第4章 複素関数の積分
- 1 複素関数の線積分
- 2 線積分の具体的な計算
- 3 コーシーの積分定理
- コラム コーシーの積分定理の証明
- 4 コーシーの積分公式
- 5 複素関数の解析関数
- 6 リーマン面
- コラム 最大値の原理
第5章 ローラン展開と留数定理
- 1 ローラン展開
- 2 留数定理
- 3 留数定理の実関数の定積分への応用
- コラム 代数学の基本定理
- 独学で複素関数(解析)を理解したい人
- 大学の講義で複素関数(解析)を理解できなかった人

名前通り、1冊で複素関数を初学者レベルをマスターできます。
2位 複素関数キャンパス・ゼミ (マセマ)
| 難易度 | 初学者向け | |
| わかりやすさ | 図が多くわかりやすい | |
| 単元の網羅性 | 初学者には十分 |
- 大学生が1番使っているマセマシリーズ
- 数式(途中式)の解説が丁寧
- 式を図形的に表現しているからわかりやすい
- 高校数学・大学数学の基礎の復習も手厚い
- 本題に入るまで分量が多く、少し混乱する部分がある
講義1 複素数と複素数平面の基本
(複素数と複素数平面;複素数の極形式 ほか)
講義2 さまざまな複素関数
(複素関数と2つの複素数平面;整関数・1次分数関数 ほか)
講義3 複素関数の微分
(複素関数の微分と正則関数;コーシー・リーマンの方程式(C‐Rの方程式) ほか)
講義4 複素関数の積分
(複素関数の積分;コーシーの積分定理 ほか)
講義5 複素関数の級数展開
(ベキ級数とテーラー展開;ローラン展開 ほか)
付録 代数学の基本定理
- 数学が苦手な人
- 高校・大学数学の基礎から学習したい人
3位 テキスト複素解析
| 難易度 | 初学者向け | |
| わかりやすさ | 1部丁寧じゃない所がある | |
| 単元の網羅性 | 初学者には十分 |
- 重要項目のみをpick up
→速く複素解析をマスターできる
- 分量が他の2冊の約1/3
- 簡潔に書かれていてわかりやすい
Chapter 1 複素数と複素関数
§1 複素数と複素平面・1
§2 複素数と複素平面・2
§3 複素関数
§4 指数関数・対数関数
§5 三角関数
Chapter 2 正則関数
§6 複素関数の微分法・1
§7 複素関数の微分法・2
§8 複素積分
§9 コーシーの積分定理
§10 コーシーの積分公式
Chapter 3 級数展開
§11 ベキ級数・テイラー展開
§12 ローラン展開と特異点
§13 留数定理
§14 実積分への応用・1
§15 実積分への応用・2
演習問題の解または略解
- 細部を抜きにして、速く複素関数(解析)を理解したい人
2. 演習用・定期テスト対策

次に、演習用・定期テスト対策用の問題集について紹介していきます。
このセクションでのターゲットとランキングの基準は以下の通りです。
- 基礎が理解できている人
- 院試や定期テストを見据えて、問題演習したいと思っている人
- 解説が丁寧で中級者が理解しやすいもの
- 問題の質 (院試や定期テストで頻出な良問)
- 問題量と単元の網羅性
1位 弱点克服大学生の複素関数
| 難易度 | 基礎から応用 | |
| 解説の丁寧さ | ちょうどいい丁寧さ | |
| 問題の質 | 試験典型問題多数 | |
| 問題量 | 約大問130問 | |
| 単元の網羅性 | 院試にも十分 |
- 左ページに基本事項の解説
右ページに問題の解説というスタイル
- 解説が程よく丁寧で見やすい
- 図も適宜用いられており、わかりやすい
- つまづきそうな所も補足で丁寧に解説
- 基礎的な参考書にはない範囲も網羅
- 1 複素数・複素平面と、関連する基本事項
- 2 複素関数
- 3 正則関数
- 4 有理型関数
- 5 留数定理とその応用
- 6 発展的な話題
- 院試対策
- 定期テスト対策
2位 演習 複素関数キャンパス・ゼミ (マセマ)
| 難易度 | 基礎的 | |
| 解説の丁寧さ | 丁寧 | |
| 問題の質 | 基礎的な問題 | |
| 問題量 | 大問約120題分 | |
| 単元の網羅性 | 中級者には十分 |
- 大学生が1番使っているマセマシリーズ
- 1大問1ページ以上の丁寧な解説
- 丁寧な数式(途中式)解説
- 全問ヒントが書かれている
→いきなり答えを見ずに取り組める
- 各公式の証明問題も多い
→いいアウトプットになる
講義1 複素数と複素数平面の基本
(複素数の計算;複素数の実数条件 ほか)
講義2 さまざまな複素関数
(w=f(z)の写像
1次分数関数 ほか)
講義3 複素関数の微分
(導関数の定義式;C‐Rの方程式 ほか)
講義4 複素関数の積分
(複素関数の線積分;コーシーの積分定理 ほか)
講義5 複素関数の級数展開
(テーラー展開;マクローリン展開 ほか)
- 定期テスト対策
- 初歩的な問題のアウトプットをしたい人
3. 院試実践向け (院試問題集)

最後に、院試実践向けの問題集を紹介していきます。
これから紹介する問題集は、複素関数(解析)以外の問題も収録されています。
なので、他の数学の院試対策にもなります。
ランキングの基準は以下の通りです。
- 地方国公立~旧帝大レベル向けのもの
- 解説の丁寧さ
- 問題の質
- 問題量と単元の網羅性
1位 詳解 大学院への数学 理学工学系入試問題集
| 難易度 | 地方国公立~旧帝大レベル | |
| 解説の丁寧さ | やや簡潔 | |
| 問題の質 | 院試の典型問題多数 | |
| 問題量 | 約大問45問 | |
| 単元の網羅性 | 院試には十分 |
- 地方国公立~旧帝大まである入試問題集
- 工学系に必要な数学のほとんどが収録
- 院試の頻出問題が多い
- 工学系の入試問題が中心
- 解説は基礎ができていないとかなり厳しい
- 1. 微分方程式
- 2. ラプラス変換、フーリエ解析
- 3. ベクトル解析
- 4. 微分、積分
- 5. 線形代数
- 6. 確率、統計
- 7. 複素関数
- 8. 情報・管理工学系の数学
- 1冊で院試数学の対策をしたい人
- 工学系の院試で数学が必要な人
2位 演習 大学院入試問題集 数学Ⅱ
| 難易度 | 旧帝大レベル以上 | |
| 解説の丁寧さ | 丁寧 | |
| 問題の質 | 良問 | |
| 問題量 | 約大問50問 | |
| 単元の網羅性 | 院試には十分 |
- 東大の院試問題を中心に構成
- 東大以外の問題は旧帝大レベル
- 典型問題より応用問題の方が多い
- 1つの例題に1ページ以上の解説
- 1. ラプラス変換、フーリエ解析
特殊関数、変分法 - 2. 複素関数論
- 3. 確率統計
4編 ラプラス変換,フーリエ解析,特殊関数,変分法
4-1 ラプラス変換
4-1-1 ラプラス変換の定理
4-1-2 諸公式
4-1-3 ラプラス変換の例
4-1-4 部分分数分解とヘビサイドの展開定理
4-1-5 ラプラス変換による定数係数微分方程式の解法
例題・問題研究
4-2 フーリエ解析
4-2-1 直交関数
4-2-2 フーリエ級数
4-2-3 フーリエ積分
4-2-4 偏微分方程式の解法
4-2-5 積分方程式の解法
例題・問題研究
4-3 特殊関数
4-3-1 べき級数による常微分方程式の解法
4-3-2 ガウス,クンメルの微分方程式と超幾何関数,合流型超幾何関数
4-3-3 ルジャンドルの微分方程式と球関数
4-3-4 ベッセルの微分方程式と円柱関数
4-3-5 エルミートの微分方程式とエルミートの多項式
4-3-6 ラゲールの微分方程式とラゲールの多項式
4-3-7 楕円積分と楕円関数
4-3-8 ガンマ関数,ベータ関数
例題・問題研究
4-4 変分法
4-4-1 オイラーの方程式
4-4-2 直接法
例題・問題研究
5編 複素関数論
5-1 複素数
5-1-1 複素数
5-2 正則関数
5-2-1 微分の定義
5-2-2 微分公式
5-2-3 初等関数
5-2-4 複素数列
5-2-5 複素級数
5-2-6 べき級数と無限乗積
例題・問題研究
5-3 複素積分
5-3-1 複素積分の性質
5-3-2 コーシーの積分定理
5-3-3 不定積分
5-3-4 コーシーの積分表示(公式)
5-3-5 その他の定理
5-4 関数の級数展開
5-4-1 テイラー展開
5-4-2 ローラン展開
5-4-3 極,零点
5-4-4 有理型関数
5-5 留数
5-5-1 留数の定義
5-5-2 留数定理
5-5-3 無限遠点における留数
5-6 定積分への応用
5-6-1 有理型関数の場合
5-6-2 三角関数(複素指数)を含む場合
例題・問題研究
5-7 等角写像
5-7-1 写像と等角写像
例題・問題研究
6編 確率・統計
6-1 順列・組合せ
6-1-1 順列
6-1-2 組合せ
6-1-3 2項定理と多項定理
6-2 確率
6-2-1 事象
6-2-2 確率の基本定理
6-2-3 条件付き確率と独立性
6-2-4 確率変数
6-2-5 平均,分散,標準偏差,積率
6-2-6 主要な確率分布
6-2-7 その他の定理
例題・問題研究
6-3 統計
6-3-1 資料の整理
6-3-2 標本分布
6-4 確率過程
例題・問題研究
- 東大を受験する人
- 難しい問題を解きたい人
4. 参考書を10%OFF で買う方法

4.1 Amazon Prime Student 6ヶ月無料体験
参考書が安くなったらいいのになと思ったことありませんか?
Amazon Prime Student に登録すれば、なんと参考書を最大10%OFFで買うことができます。

私は大学生の時、約3万円分の参考書を買ったので、3000円お得になることになります。
6ヶ月間は無料体験期間として試せるので、無料で3000円もらえるようなものです。
さらに、Prime Studentは他にもたくさんのサービスを受けることができます。
- Prime Video
(映画やアニメが見放題)
- 便利な配送サービス
(お急ぎ便・日時指定など)
- Amazon Music Prime
(1億曲以上の曲をシャッフル再生で)
- Prime Before You Buy
(自宅で試着可能)
- Prime Reading
(1000冊以上の本が無料)
- Amazon Photos
(写真を容量無制限で保存)
prime studentの特典のすべては以下の通りです。
- 本最大10%ポイント還元
- Prime Video
(映画やアニメが見放題) - 便利な配送サービス
(お急ぎ便・日時指定など) - Amazon Music Prime
(1億曲以上の曲をシャッフル再生で) - Prime Before You Buy
(自宅で試着可能) - Prime Reading
(1000冊以上の本が無料) - Amazon Photos
(写真を容量無制限で保存) - 対象の文房具・ノートの割引
- ソフトウェアの対象商品割引
- Amazon MastercardでAmazonポイントが2%たまる
- お得なセールをいち早くチェック
- Amazon フレッシュ
- 無料体験期間が6か月
それぞれの特典やprime studentについてさらに詳しく知りたい方は以下の記事をご覧ください。
4.2 登録方法
① Prime Student 会員の登録ページにアクセスする
② 今すぐ開始をタップする

③ Amazonのアカウントにログイン
メールアドレスやパスワードを記入して、ログインします。
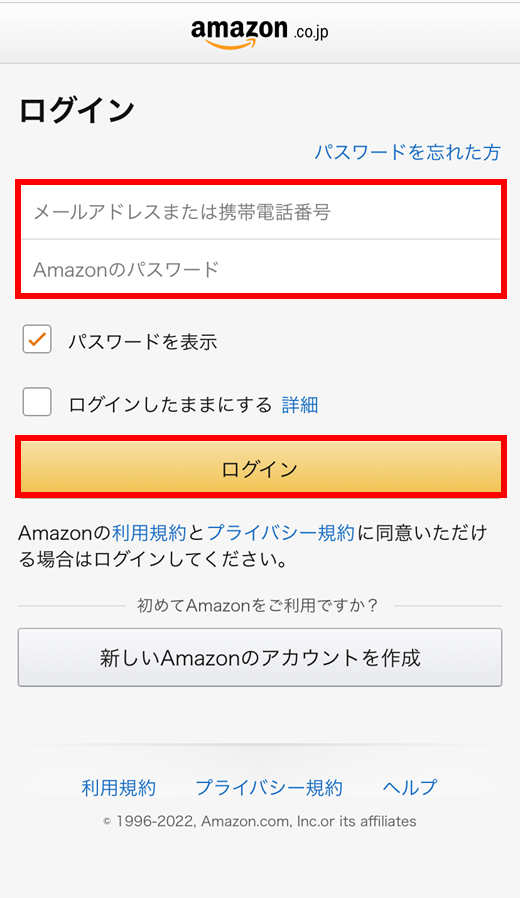
(ⅰ) 新しいAmazonのアカウントを作成をタップします。

(ⅱ) 氏名、メールアドレス、パスワードを記入して、次に進むをタップします。
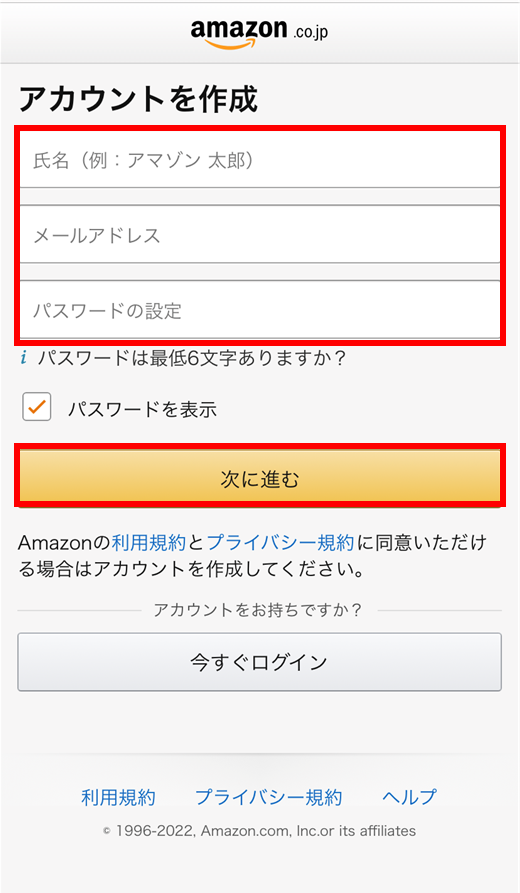
(ⅲ) 先程記入したメールアドレスに確認コードが届くのでそちらを画面に従って記入して下さい。
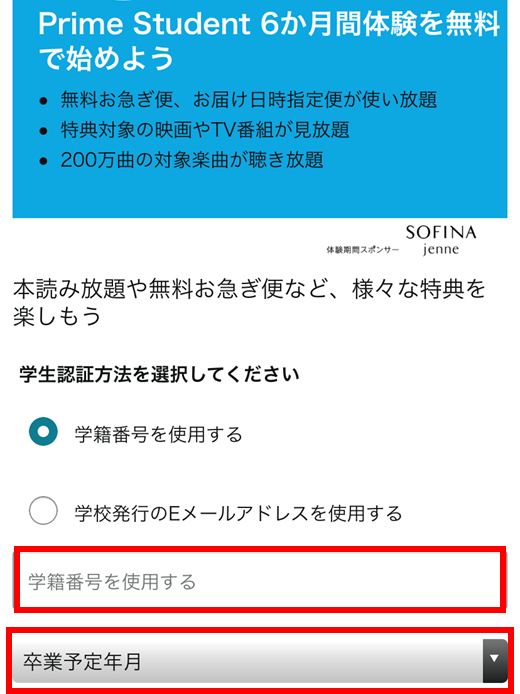
④ 学生認証
(ⅰ) 学生認証方法を選び、記入して下さい。
(ⅱ) 卒業予定年月を選択して下さい。
⑤ お支払い方法の選択と記入
お支払い方法を選択し、それぞれの指示に従って必要事項を記入して下さい。
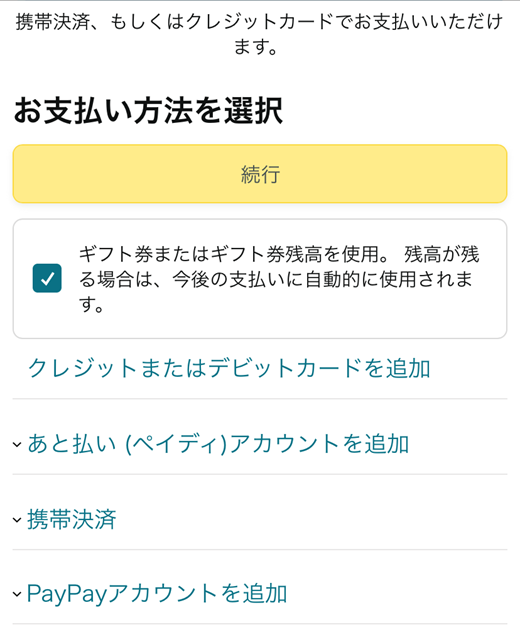
記入が終わったら、6ヶ月の体験期間を試すをタップすれば登録完了です。
5. 迷ったらこれ

5.1 初学者

簡単にかみ砕いて説明されているので、とてもわかりやすいです。
5.2 演習用・定期テスト対策

解説が程よく丁寧で見やすく、院試対策にも対応できます。
5.3 院試実践向け (院試問題集)

院試の頻出問題が多く、工学系に必要な数学のほとんどが収録されています。










